Table of Contents
1.2: The Top Level Function and HLS Data Types
In this section, we'll explore our top level function and dive into some of the unique data types used by HLS. A thorough understanding of how HLS functions work is essential to creating your own design.
1.2.1: GetCentroid: The Top Function
Take a look at the file GetCentroid.cpp. The top level function is defined as follows:
void GetCentroid(hls::stream<uintSdChIn> &inStream, fp_data_t IndArr[WAVESIZE], fp_data_t *Centroid)
In this definition are two different data types that may not be familiar to you if you haven't used Vivado HLS before (the latter type is actually defined in includes.h). If that's the case, don't worry, we'll discuss both of those data types in turn in the following sections.
What's very important to note here is that the name of our top-level function for our design needs to match the function name we defined in the Project Settings. If the Synthesis window in the Project Settings doesn't look like this:
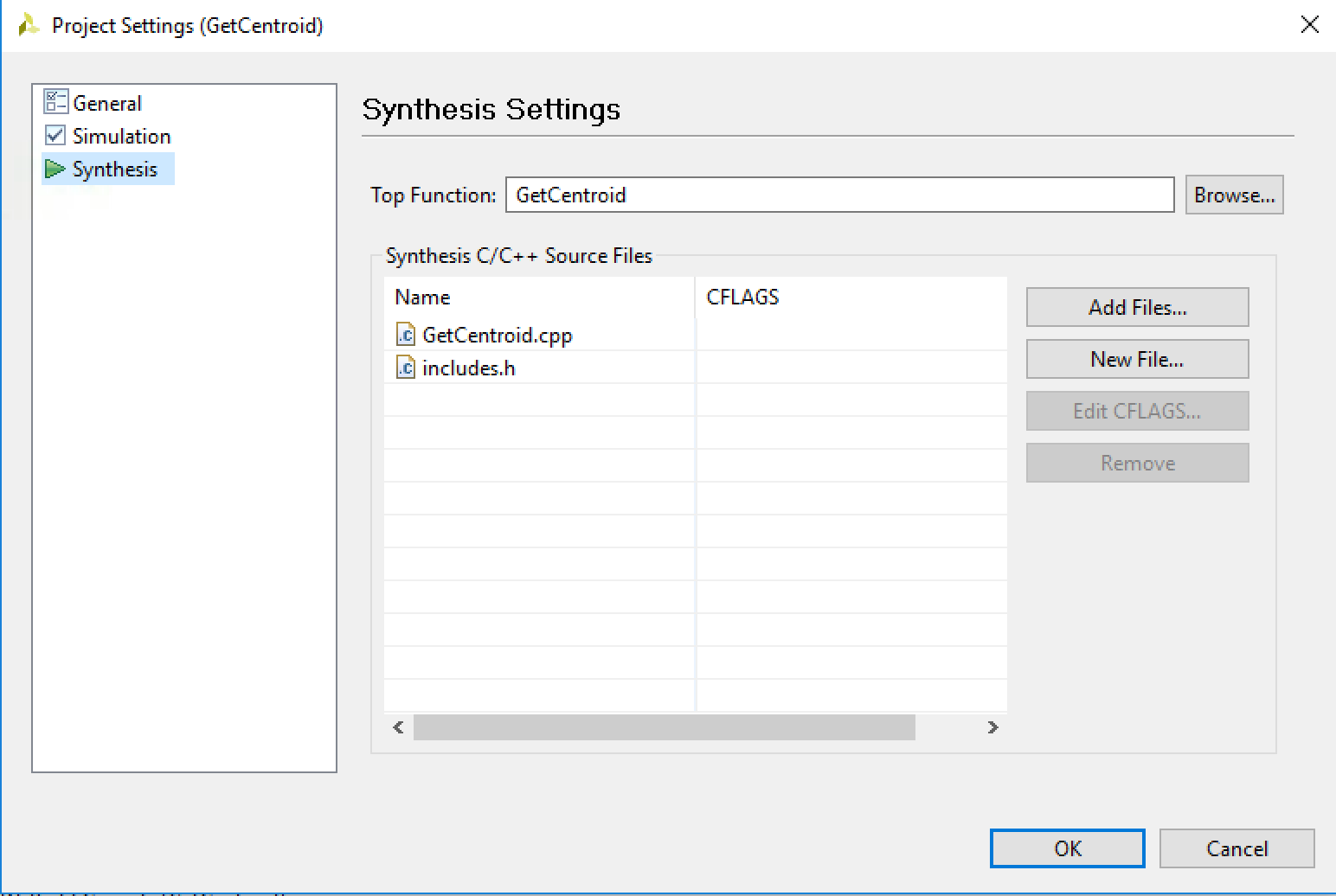
you will have no luck synthesizing your design. So make sure your Top Function name in your Synthesis Settings matches up with the one in GetCentroid.cpp. They should both be GetCentroid in this case.
1.2.2: The HLS Stream Argument
The hls::stream identifier is one that you'll see frequently throughout examples of HLS code. It represents a FIFO-based data transfer that requires no address management and offers side-channel information. I'd recommend at least browsing the HLS Stream Library section in Chapter 2 of UG-902 at this point. I'll just cover some basics of why we're using it here and what it entails.
The main reason we're going with the HLS Stream here is that it's the natural choice for connecting to the Direct Memory Access engine on the Zynq, and we're going to be using DMA to move data from the processor into the Programmable Logic (PL). DMA is a powerful and ubiquitous concept for modern processors, so if you aren't familiar with I suggest you read up.
One of the things you'll immediately notice is that there is no pre-defined size for the hls::stream input! That can create some confusion when you're writing your code since it's up to you as the coder to make sure that your algorithm gets the amount of data it expects. If it doesn't, it will just hang and you won't really have any idea what went wrong.
1.2.2.1: Defining the HLS Stream Type
Notice that when we declare the inStream argument as type hls::stream<uintSdChIn>,
hls::stream<uintSdChIn> &inStream;
we're declaring it using a template with data type uintSdChIn, which is defined in includes.h as
typedef ap_axiu<32,1,1,1> uintSdChIn;
(this assumes that we've defined NUMCHANNELS as 2; more on that later). This is basically just an ap_axiu type (Yes, I know this requires a lot of digging through many strata, but that's the basis of the game). The definition of ap_axiu occurs in the ap_axi_sdata.h header file, and it looks like this
template<int D,int U,int TI,int TD>
struct ap_axiu {
ap_uint<D> data;
ap_uint<D/8> keep;
ap_uint<D/8> strb;
ap_uint<U> user;
ap_uint<1> last;
ap_uint<TI> id;
ap_uint<TD> dest;
};
So when you put all this together, you can see we are going to be using an hls::stream with 32-bit data elements since we are setting D=32. We are setting U=1, TI=1, and TD=1 since we aren't actually going to use the side-channel information. I haven't written an application that requires this side-channel information; chances are you won't need it. Note that the template forces at least one bit to be devoted to the TLAST signal.
1.2.2.2: Writing and Reading from the HLS Stream
Now, in the real hardware design, we aren't going to have to explicitly "write" to the HLS Stream. The "write" is going to be a DMA burst from the DDR memory to the PL. However, for the case of simulating our design in HLS, we write to the HLS Stream in the testbench using some code that looks like this:
uintSdChIn valIn;
valIn.data = 100;
inputStream << valIn;
You'll see something very similar in TestGetCentroid.cpp. In case shown above, we are simply writing the value of 100 into one of the 32-bit slots. Again, you can only push stuff into the top, you can't write to an arbitrary address. It helps if you remind yourself that, physically, the HLS Stream isn't memory. Think of it more as a FIFO of infinite depth.
When it comes to reading from the stream, we do it with a sequence like this:
uintSdChIn valIn;
ap_uint<32> value;
valIn = inStream.read();
value = valIn.data;
That's how we pull data elements from the stream in GetCentroid.cpp. Again, you can't access arbitrary elements; only the first off the top.
1.2.2.3: Pipelining Our Main For Loop
One of the the most important concepts in HLS—and FPGA designs in general—is "pipelining". The ability to pipline operations is what really gives FPGAs an edge above regular microprocessors. Why is this? Well, simple microprocessors can only really perform one operation on a given clock cycle. FPGAs, on the other hand, can perform a number of different logical operations on the same exact clock cycle since all the logic blocks are doing things simultaneously.
In HLS, we can pipeline all the operations in a for loop by using the PIPELINE pragma. Notice the lines
for (i=0; i < (WAVESIZE/NUMCHANNELS); i++){
#pragma HLS PIPELINE
We put the pragma directly below the for loop declaration. There is another way to do this using the Directive tab at the far right of the console, but I'm not going to cover that.
If you're not familiar with this concept, think of a simple for loop where we first add a number, a, to our input and then multiply the result by a constant, b. If we pipeline these operations, on the first clock cycle, the hardware will add a to the first element. On the second clock cycle, it will both add a to the second element and multiply the previous result by b. Analogies and drawings are really helpful to illustrate this concept. UG-902 has some good figures. If that doesn't work for you, I came up with an analogy about ordering drinks at a bar that may help make things clearer.
1.2.2.4: Packing Multiple Values into the Input Stream
You may be curious what this NUMCHANNELS business is all about. The simple answer is that we are going to be packing multiple 16-bit numbers into one uintSdChIn: two in this case. If you look through the code, you'll notice there is a nested for loop where we iterate over these two channels (with the variable j) and pull out the two packed values using the following syntax:
dataIn = value.range((j+1)*16 - 1, j*16);
Why do we do this? Well, we are taking advantage of the fact that the DMA burst can handle 32 electrical signals simulataneously, so two 16-bit values can arrive at exactly the same time as input to our algorithm in hardware. When we nest the for loop inside a pipelined loop, Vivado HLS automatically "unrolls" it, which essentially means it creats two identical copies of the hardware (if it can) to carry out the operations in the nested loop in parallel.
If that sounds confusing, see this nice response to the question I asked on the Xilinx Forum and read up on unrolling loops in UG-902.
1.2.3: The Fixed Point Data Type Argument
The other two input arguments to GetCentroid are of type fp_data_t. Inside includes.h, you'll see that this is a type we've defined ourselves as
typedef ap_fixed<BW,IW> fp_data_t;
the ap_fixed template is defined in ap_fixed.h and represents a fixed point number. "Why are we dealing with fixed point numbers?", you may ask. Well, if you're a software engineer trying to learn how to program FPGAs, it may be quite some time since you learned about floating point numbers and you might have started to take them for granted like most of us do. So it's a reasonable question to ask.
The thing is, floating point arithmetic is a bit messy and it takes time. And sometimes, it's more precise than we actually need. For instance, if we are working with ADU values from a digitizer and the noise is three or four counts, it really doesn't make much sense to try to calculate a mean down to the thousandths. So one of the ways to speed things up is to used fixed point numbers and fixed point arithmetic.
The template for the ap_fixed type requires two numbers. You'll also that we've set these numbers, BW and IW, to be
#define BW 32 // Total number of bits in fixed point data type
#define IW 24 // Number of bits left of decimal point in fixed point data type
As you can see in the comments, our choice means that our fixed point number will have 32 bits total, and 24 bits to the left of the decimal point. But be careful! That's not "24 places". That's 24 bits. I'm not going to get into the nitty-gritty details about fixed point numbers, but essentially what this means is that the lowest resolution of the number that can be represented is 2-8 = 0.00390625. The largest number that can be expressed is 223=8,388,608. What about the other bit, you ask? That's for the sign (or the MSB in two's complement). If you want to use unsigned fixed point numbers to get that extra bit of precision, you can use the ap_ufixed template that's also defined in ap_fixed.h.
The other two arguments to our function are both fp_data_t data types. The first is an array of 256 elements and the second is a pointer to the value that is calculated and returned by GetCentroid.
1.2.4: So...What does our function do?
It may not be immediately clear what our function is actually doing if you've never calculated a centroid or center of mass before, but this is a pretty standard calculation in physics (see the HyperPhysics example). Basically what we're doing is adding up all of our input array values and also adding up the those values after being weighted by the values in IndArr (which just happens to be an array of indices from 0-255 in our case, but could be a more complicated set of weights).
At the end, we divide the latter by the former to get our center-of-mass. You can write a simple script to prove to yourself that the center of mass of this index array is 170.333 repeating. Since we are using fixed point numbers with a minimum resolution of 0.00390625, we can't quite there. But we should get an answer somewhere around 170.33333, to about the third decimal place. To return our answer, we use a pointer to the ap_fixed value Centroid, which is one of the arguments of our function, and pass that by reference to the caller.
1.2.5: Returning Values by Reference
Pretty much every example I've found of an HLS function that uses an input HLS stream returns an output stream that has an equal amount of elements as the input. In fact, it drove me nuts trying to return a stream that had less elements than the input! Nowhere in the documentation or forums could I find any indication that this should be impossible, but all my efforts proved that it was (if someone reads this and knows the secret of how to create a function that doesn't output a stream value for every input stream value, please let me know).
In our example, we are taking in 255 waveform values and we only need to return one: the fp_data_t value Centroid. We can do this by passing it by reference in our top level function. When we synthesize everything and build it into our design, we'll find that we can obtain the return value by simply reading a register in the PL after we receive an interrupt telling us its ready. We'll cover that topic in depth in Chapter 3, Section 3. Right now we're going to get into how we test and synthesize this algorithm.
← Previous ... Next →